Uniform Circular Motion - Topic 6.1

Bite-sized Uniform Circular Motion Study Notes for IB Physics HL/SL

Circular Motion and Angular Speed

Key points

Circular motion is when an object moves along the circumference in a circle.
The period is the amount of time it takes for the object to complete one full revolution.
Angular speed is equal to the change in angular rotation over the change in time, measured in radians per second.

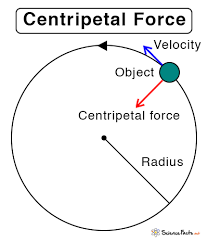
Circular Motion is the motion of an object in a circular path, such as the cornering of a car.

The period, T, is the amount of time the object takes to complete one revolution around the circle.
The linear velocity depends on distance/time.
- Assuming that the period T is the timeframe, and the distance is the revolution of the circle, we get the equation to the right:
  - This is for the velocity along the circumference of the path, or the linear speed.

Not in Formula Booklet but important

The angular speed refers to the rate at which the object turns.

The angle swept by the object divided by the time taken to do so.
It is measured in radians per second.
The linear speed is equal to the angular speed times the radius (in the formula booklet).
- This leads to the second formula in the example to the left.

The angular speed vector is tangent to the circumference of motion.

If the force was no longer applied, the motion of the object would follow that tangent.

Key points

In uniform circular motion, even if the linear velocity is constant, the angular velocity changes because the direction of the motion changes.
- This change of velocity means that there is acceleration.
  - This is called centripetal acceleration.
The direction of centripetal acceleration is always towards the center of the circle.
- The magnitude of the acceleration is constant if the linear velocity is constant.

Centripetal Acceleration is the change of velocity that takes place within uniform circular motion.

From the motion unit, recall that acceleration occurs whenever the velocity changes.
- In circular motion, the direction of motion changes as the object travels along the circumference.
  - Velocity is a vector, so it changes as direction changes.
    - If the velocity vector changes, then there is acceleration.
The direction of this acceleration is towards the center of the circle.
- The centripetal acceleration vector is normal (perpendicular) to the velocity vector.
The magnitude of the acceleration is constant if the linear velocity is constant.

Formula Booklet

These are the formula booklet equations for centripetal acceleration.

Key points

Centripetal acceleration and velocity are caused by centripetal forces.
- The direction of the force is towards the center of the circle.
Centripetal forces are the net forces that cause uniform circular motion.

Centripetal Forces are the net forces that act towards the center of the circle and cause circular motion.

Centripetal forces will be stronger with higher acceleration and velocity, as well as mass.
Radius also has an influence – a smaller radius means a “tighter” circle and a greater centripetal force.
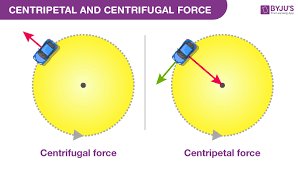
Note: There is a difference between centripetal and centrifugal forces, as seen in the second image to the right.

Formula Booklet

The formula booklet equation is to the right.

From Newton’s Second Law, we know that F=ma, so the force can be calculated by multiplying the mass of the object by the centripetal acceleration.
- Use the first formula if using linear velocity, and the second for angular velocity.
In word problems, use calculated values for centripetal force in combination with forces like friction, weight, and reaction forces.

Subscribe to the Inertia Newsletter

IB News, Covid-19 Updates, Deadlines, Tips and Tricks, and Hundreds of Free Resources are Awaiting You!